Вещественными или действительными числами исчисляется все, что (простите за тавтологию) существует в действительности. Иными словами — все что есть, а так же все, что можно себе представить или вообразить. Примеры приводить не буду — это уже где-то на грани идиотизма… Впрочем это и 0, и 1, и -2, и бесконечность, и миллион, и число «пи» и… И так далее. Cм. рисунок, где прямая ОХ представляет из себя вещественную ось. Полагаю, хватит об этих числах.
Комплексными числами вообще не понятно что исчисляется. По крайней мере я не скажу. Да и никто не скажет. У меня на сей счет имеется версия — числами этими исчисляется все, что вообразить ну уж никак нельзя. То есть, если брать наш случай, числа означенные решительно подходят для исчисления Бога. Нужны еще примеры? Извольте. Вы понимаете, как самолеты летают? Лично я — нет! Для меня это за гранью добра и зла и, вообще, - здравого смысла. Ну, посудите сами — несется этакая дура в сотню тонн по эфимерному воздуху. Почему не падает? Загадка! И немудрено. Расчет подъемной силы, сопротивления крыла, по крайней мере в наше время, производится с применением функции Жуковского. А функция эта из комплексного анализа… Короче — неиспорченному абстракциями уму непостижимо и невообразимо это всё.
Для умов же испорченных привожу легкие математические подробности. Впрочем, подробности эти будут всем полезны, так как в дальнейшем только добавят наглядности к излагаемому.
А что, собственно, есть поле? Лапидарненько так, на примере поля вещественных чисел. Что имеем? Две операции: сложение и умножение. Два особых элемента со специфическими свойствами: 0 и 1. Наличие у каждого ненулевого элемента обратного (как по сложению так и по умножению, например, соответственно: 5 и -5, 5 и 1/5). Что еще… Ах, да — замкнутость по двум основным операциям, то есть, {элемент поля} (плюс или умножить) {элемент поля} = {элемент поля}. Сэ ту. Вся правда, несколько сложнее, но для краткого введения достаточно.
Рассмотрим множество (назовем его C) упорядоченных пар действительных чисел z = (x, y) или, что то же самое, точек декартовой плоскости xOy или свободных плоских векторов (см. рисунок). Так вот — если операцию умножения элементов этого множества ввести особым образом, то такое введение превращает множество C в поле, которое называется полем комплексных чисел. Не буду расписывать эту операцию — для нас, здесь, это не важно. Достаточно будет сказать следующее — умножение элементов в поле C, в глубинной сути своей, символизирует поворот вокруг начала координат комплексной плоскости. Не подумайте обо мне плохо - это не строгое определение, это… Убогая попытка как-то философски осмыслить, что-ли.
Да… Туманно все. Неясно… Ладно! Вот смотрите. Все очень просто. На пальцах. У нас есть плоскость. Так. У плоскости два измерения (грубо говоря - по горизонтали и по вертикали). Так? Каждое из измерений связываем с прямой. Горизонтальное - с OX, вертикальное - с OY. Это элементарно! Это всякому плотнику понятно. Затем. Вводим на прямых градуировочные деления (для удобства измерений в данной плоскости). И сие тоже очевидно. Это как линейки приложить. Одну линейку приложили к OX, другую - к OY. Но. У каждой из линеек должна быть единица. Эталонное деление. Линейка, простите, ведь тоже может быть как в сантиметрах, так и в дюймах.
Положим мы створки шкафа на листе ватмана проектируем. Законно можем ввести две единицы измерения: «сантиметр горизонтали» и «сантиметр вертикали». Причем в дальнейшем имеем право задать им разные размеры: одному, допустим, семь милллиметров, а другому - двенадцать. Мало ли… Может нам для чего-то надо масштаб итогового изделия гротескно перекосить…
Так вот: на OX эту «единицу», это «эталонное деление» так и назвали 1. Единица. Но на OY оно должно иметь иное название. Почему? Зачем? Чтобы мы имели полный контроль над всеми операциями. Чтобы мы четко знали что и с чем мы складываем или что на что умножаем. Дабы в громоздких геометрических вычислениях, при упрощении многочленов, в которых коэффициенты длины (по OX) и высоты (по OY) сложно перемешаны, не запутаться. На сем основании (не долго думая) это самое «эталонное деление», эту «единицу» на OY назвали i. Могли назвать как угодно e, b, j… Но назвали i. Так уж исторически сложилось. Надеюсь, пока, все ясно?
Ну-с… Что в итоге имеем? Два множества вещественных чисел (наши прямые OX и OY). Одно градуировано в долях единицы, другое - в долях i. То есть, например, число 777,333 во множестве OX запишется как 1 * 777,333 (обобщая: 1 * x), а во множестве OY - как i * 777,333 (обобщая: i * y). Итак, наличествует два множества. Но вот вопрос: как получить из них третье? И не просто третье, а некоторым образом включающее оба исходных? Есть способ! Декартово произведение множеств. Не будем вдаваться в подробности - в нашем случае это (если элемент нового множества назвать z): z = {элемент одного множества} + {элемент другого}. Или z = 1 * x + i * y. Или (мы ведь не полные маразматики - единицу в умножении можно и опустить) z = x + iy!
Причем, обратите внимание - «плюс» здесь не совсем тот, что, к примеру, в выражении 2 + 2. В 2 + 2 складываются элементы одного множества, а в x + iy - разных. Посему «плюс» в последнем двучлене это не понуждение к выведению итоговой суммы, а всего лишь знак элемента iy. То есть вся конструкция, не что иное как z = (x, +y). Впрочем, «плюс» в последнем варианте записи числа z как правило опускается.
Что теперь получилось? Некое множество, образованное декартовым произведением двух множеств действительных чисел. В просторечии это - точка плоскости и ее координаты. Вся то и премудрость, что записано хитро - столяр пишет тоже… фиг прочтешь, через закорючку, на клочке бумаги, а мы - через плюс, вот так: z = x + iy. Что напоминает? А ведь заметьте, ни о каких комплексных числах пока и речи не шло. В чем фокус?
Зачем превращать множество в поле? В поле больше возможностей для использования всей полноты математики, для построения красивых теорий, для «открытий чудных…»
Фокус последует сейчас. Следите за… (чуть не сказал - руками). У нас есть множество точек плоскости, вида z = x + iy. Мы хотим превратить это множество в поле. Что для этого нужно? Практически лишь одно - нужно ввести в этом множестве операцию умножения элементов. Но так, чтобы операция эта не противоречила аксиомам поля. И в предложенных обстоятельствах ЭТО МОЖНО СДЕЛАТЬ ТОЛЬКО ОДНИМ СПОСОБОМ.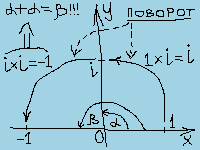 
А ИМЕННО. Если перемножать z1 = x1 + iy1 и z2 = x2 + iy2 как двучлены по обычным законам алгебры (вот где проявляется важность разных обозначений для единиц OX и OY, иначе запутались бы). ДА! НО... НО ПРИ ЭТОМ ПОЛОЖИТЬ i2 = -1!!! ТАК И ТОЛЬКО ТАК! В чем гениальность сего положения? ПОВОРОТ! Вид перехода из суб-поля в суб-поле, из оси в ось! Умножение здесь суть поворот, при котором углы сомножителей складываются! Тут масса открытий-следствий, но первейшее это то, что умножение, в некотором роде, заменяется сложением, то есть появляется экспонента, а это влечет такие последствия, что… Короче - именно так введенное умножение элементов z превращает их множество в поле комплексных чисел и рождает все сказочное и не сразу постижимое многообразие комплексных алгебры и анализа!!!
Утомил? Простите великодушно, интеллектуальные мои. Это я писал скорее для себя (и для таких же «умников», как я сам). Охота ведь все-таки хоть самую малость разобраться…
Далее (чуть-чуть, чисто для формальности)… Элементы множества C — векторы z = x + iy — называются комплексными числами. Таким образом, комплексное число z = (x, y) представляет собой упорядоченную пару, комплекс, составленный из действительных чисел x и y, которые (в дань исторической традиции) соответственно называются действительной и мнимой частью числа z и обозначаются символами x = Re z, y = Im z. Числа z = (0, y), действительная часть которых равна 0 (в дань той же традиции) , называются мнимыми. Это как раз и есть наша мнимая единица, наше i. То есть, строгости ради, число i, представленное нами как комплексное, как комплексное и надо было бы записать, а именно — 0 + i * 1. Но…
Не будем усложнять, дабы не мучить неискушенных зрителей. Зрителей этой новой, и все же очередной, драмы. Драмы поиска Единого БОГА.
